Next: Equações constitutivas Up: Magnetismo da matéria Previous: Introdução

A magnetização

No vácuo, para correntes estacionárias, sabemos que

$\begin{displaymath} rot \vec{B}=\frac{4\pi}{c}\vec{j} \end{displaymath}$

(1)

Na presença de matéria podemos imaginar que o campo magnético vá afetar, ou mesmo criar, correntes microscópicas (por exemplo, pelo mecanismo da indução eletromagnética). Consideremos um material condutor, como um ímã em forma de barra. Como não existe um circuito fechado, não pode haver correntes estacionárias macroscópicas. No entanto, pode haver correntes microscópicas. Suponhamos que estas sejam descritas por uma densidade de corrente $\vec{j}_m$ , onde o índice

significa microscópico. Logo, podemos precisar melhor a equação acima. Ela será:

$\begin{displaymath} rot \vec{B}=\frac{4\pi}{c}\vec{j}_m \end{displaymath}$

(2)

Essas correntes não trasportam carga (fazem-no de um ponto para o outro do átomo, mas não macroscopicamente). Em qualquer seção do condutor, portanto, teremos

$\begin{displaymath} \int \vec{j}_m.\vec{n}dS=0 \end{displaymath}$

(3)

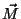Consideremos esta última relação como uma equação, $\vec{j}_m$ sendo a incógnita. A solução trivial é $\vec{j}_m=0$ . Será ela a única? Não. Seja $\vec{M}$ um campo vetorial nulo fora do condutor e tal que

$\begin{displaymath} \vec{j}_m=c\;rot\vec{M} \end{displaymath}$

(4)

Tomemos uma superfície qualquer $\Sigma$ que corte o condutor e prolonguêmo-la um pouco além da superfície do condutor.

$\begin{pspicture}(0,0)(10,6) \psline(2,2.5)(3.7,2.5) \psline(2,4)(3.7,4) \psline... ...,3.25)(3.7,2.5) \uput[0](4.5,4.6){$c$} \uput[0](3.8,3){$\Sigma$} \end{pspicture}$

Seja

a curva que é a fronteira dessa superfície, como mostra a figura. Orientemos

escolhendo um sentido de percurso e escolhamos uma normal à superfície $\Sigma$ cujo sentido esteja coordenado com o sentido de percurso na curva pela regra do saca-rolhas. Então,

$\begin{displaymath} \int_{\Sigma}\vec{j}_m.\vec{n}dS=c\int_{\Sigma}rot\;\vec{M}.\vec{n}dS= c\oint_{c}\vec{M}.\vec{dl} \end{displaymath}$

(5)

pelo teorema de Stokes. Ora,

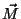é externa ao condutor, e $\vec{M}$ é, aí, zero. Logo,

$\begin{displaymath} \int_{\Sigma}\vec{j}_m.\vec{n}dS=0 \end{displaymath}$

(6)

É claro que esta solução generaliza a solução trivial, que é obtida para $\vec{M}=0$ .

Voltando à Eq.(2), temos, agora,

$\begin{displaymath} rot\;\vec{B}=\frac{4\pi}{c}c\;rot\;\vec{M} \end{displaymath}$

(7)

$\begin{displaymath} rot(\vec{B}-4\pi\vec{M})=0 \end{displaymath}$

(8)

Definindo um novo campo 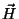$\vec{H}$ como

$\begin{displaymath} \vec{H}=\vec{B}-4\pi\vec{M} \end{displaymath}$

(9)

temos

$\begin{displaymath} rot \; \vec{H}=0 \end{displaymath}$

(10)

quando as únicas correntes presentes são as microscópicas (também chamadas ``correntes de magnetização'' ou ``correntes de Ampère''). Enquanto $rot\;\vec{B}=\frac{4\pi}{c}\vec{j}$ diz que, sempre que existe uma corrente (macroscópica ou microscópica) existe um $\vec{B}$ , a relação (10), ou, para ser mais completo, a relação equivalente

$\begin{displaymath} rot \; \vec{H} = \frac{4\pi}{c}\vec{j}_M \end{displaymath}$

(11)

(onde $\vec{j}_M$ é a densidade de corrente macroscópica) diz que, sempre que houver uma corrente macroscópica, haverá necessariamente um 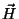$\vec{H}$ . Ou seja, 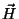$\vec{H}$ está relacionado às correntes macroscópicas da mesma forma que $\vec{B}$ está relacionado à corrente total. Uma forma imprecisa¹ , mas útil (por ser mnemônica), de dizer isto é a seguinte: enquanto qualquer corrente é fonte de $\vec{B}$ , só as correntes macroscópicas são fontes de $\vec{H}$ .

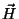Next: Equações constitutivas Up: Magnetismo da matéria Previous: Introdução

Henrique Fleming 2002-12-24